返朴 2019-04-12 作者:曹则贤
引力偏折光线缘起牛顿研究光学而来的疑问,然后引力偏折光线的偏折角就被德国人索尔德纳当个重物的引力散射经典问题给计算了。后来,德国人爱因斯坦从1911年经1915年用不同成熟度的广义相对论一路计算到了1936年最终提出了引力透镜的概念。 1919年英国人爱丁顿的日蚀照片宣称精确测量了光经过太阳附近的偏折角从而“验证”了广义相对论,一举将爱因斯坦送上了神坛。1979年,实在架不住人们对爱丁顿处理照片数据的强烈质疑,英国组织了对爱丁顿照片数据的再处理,结论是“爱丁顿的结果是合理的”。通过计算照片“验证”广义相对论的说法,此乃为其滥觞。
撰文 | 曹则贤(中国科学院物理研究所)
1
光线的直与弯
光走直线,这是几何光学的基本出发点。雨后云边直射的阳光给我们以光线(射线、直线)的印象。然而,光线又是可以弯折的。观察水中直立的芦苇和游动的鱼儿,容易得出光线在水面处弯折(refraction,中文译为折射)的结论。光的反射和折射是自然现象,其规律早已为人们所掌握。光在水面处弯折,那是因为两边的空气和水是两种不同的物质。不同物质弯折光线的能力由其折射率所表征。倘若光线经过的空间中折射率连续变化,光线就会被连续弯折,或者说是沿着一条光滑曲线传播。光线沿直线传播的观念,在人类还无意识的时候就已经嵌入到我们的视觉诠释体系中了。不管光线经过怎样的波折到达我们的眼底,我们一概按照光沿直线的规律去构造那个可能的光源。水底的鱼儿反射的光,经过水面折射后进入我们的眼睛,我们会按照光沿直线传播的规律搜寻作为光源的那条水底的鱼儿。在鱼叉无数次错过了目标后,人们总结出了水里的鱼儿在我们看到的位置前下方的结论(图1)—是光沿直线传播后进入我们眼睛的这种浅薄认识误导了我们的视觉判断。沙漠中容易遇到海市蜃楼,那是因为地表空气密度连续、大范围地变化,是远处的风景(光)经扭曲后进入我们的眼睛而我们的大脑又固执地认为看到的光线都有单纯的直线传播历史才造成了这样的幻象。
光可以被物质偏转,说到底是被电磁场偏转。这不奇怪。光本身是电磁现象,是电磁相互作用的传递者(carrier)。那引力呢?引力也能偏转光线吗?
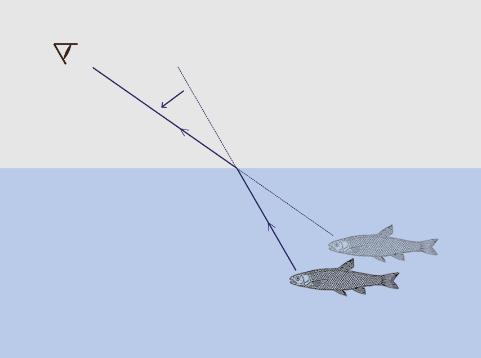
图1. 因为光的折射,我们看到的水中的鱼儿应该在我们以为的那地方的前下方
2
牛顿的疑问
牛顿研究光学,发现了阳光的光谱,还有牛顿环。 牛顿在1704年出版的Opticks(《光学》)一书中列举了自己的一些疑问,其第一条就是Do not bodies act upon light at a distance, and by their action bend its rays; and is not this action(caeteris paribus)strongest at the least distance(物体不作用于远处的光并因此弯折光线吗?这作用不是距离最近的地方最强吗)? 牛顿既研究引力,又研究光学。力学中物体的轨道是可以被外力弯曲的,光线在介质中也能被弯折,所以牛顿问这个问题一点儿也不奇怪。
物体能否凭引力弯折远处的光线,在牛顿就是个疑问,出现在其著作的queries中,在别人那里可就当成真事儿了。1784年英国人卡文迪许(Henry Cavendish, 1731-1810), 1801年德国人索尔德纳(Johann Georg von Soldner 1776-1833),都认定牛顿引力论预言了经过一个大质量天体附近的星光会被弯曲——牛顿好冤枉啊。索尔德纳的计算于1804年发表并流传至今。 1911年爱因斯坦基于等价原理计算出了和索尔德纳同样的结果。但是,在构造广义相对论的过程中,爱因斯坦于1915年认识到从前的计算结果只得到了偏转角的一半,于是又作了修正,爱因斯坦因此成为了第一个得到引力弯曲光线正确计算的人。1919年,英国人爱丁顿(Arthur Stanley Eddington, 1882-1944) 领导的探险队拍摄日全食时刻的星空照片,据说验证了引力偏折的爱因斯坦理论的正确性。这大体就是引力弯曲光线现象被提出和对待的历史简述。
3
光线偏折的计算
索尔德纳的计算结果表明,远处来的星光经一个表面处加速度为 g 的星球所造成的偏折角 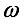 由公式
由公式 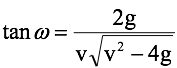 给出,其中 v 是光在星球表面的速度。 注意,那时候c还不是光速的专用符号,也没有光速不变的理念。先不谈这个公式对不对,我们首先要问的是星球的重力凭什么能让光线偏折?索尔德纳很不好意思地承认 “I treat a light ray almost as a ponderable body (我拿光当重物对待了). ” 他接着说 “That light rays possess all absolute properties of matter, can be seen at the phenomenon of aberration, which is only possible when light rays are really material. And furthermore, we cannot think of things that exist and act on our senses, without having the properties of matter(光具有物质的所有绝对性质这一点,可以从光行差现象看出,这只有光是物质性的才有可能。再说了,我们也想象不出任何事物能存在还作用于我们的感觉却没有物质的性质).” 这个,这个,这么论证就有点撒泼了。不过,索尔德纳接着说,由这个公式估算,地球甚至太阳造成的光的偏折角都太小,无法观察。他又接着论证尽管观察不到,他的计算也是有益的,因为对能观察到和观察不到之影响的认识都同样扩展我们的知识。 读到这句话时,我总想起中国人算卦的一个标准套路——两头堵,怎么说他都有理。
给出,其中 v 是光在星球表面的速度。 注意,那时候c还不是光速的专用符号,也没有光速不变的理念。先不谈这个公式对不对,我们首先要问的是星球的重力凭什么能让光线偏折?索尔德纳很不好意思地承认 “I treat a light ray almost as a ponderable body (我拿光当重物对待了). ” 他接着说 “That light rays possess all absolute properties of matter, can be seen at the phenomenon of aberration, which is only possible when light rays are really material. And furthermore, we cannot think of things that exist and act on our senses, without having the properties of matter(光具有物质的所有绝对性质这一点,可以从光行差现象看出,这只有光是物质性的才有可能。再说了,我们也想象不出任何事物能存在还作用于我们的感觉却没有物质的性质).” 这个,这个,这么论证就有点撒泼了。不过,索尔德纳接着说,由这个公式估算,地球甚至太阳造成的光的偏折角都太小,无法观察。他又接着论证尽管观察不到,他的计算也是有益的,因为对能观察到和观察不到之影响的认识都同样扩展我们的知识。 读到这句话时,我总想起中国人算卦的一个标准套路——两头堵,怎么说他都有理。
只要我们认可引力可以偏折光线,偏折角有个简单的基于量纲分析的推导,而不必管具体的物理机制或理论。笔者的思路如下。偏折角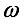 是个无量纲量。就引力偏折光路这个问题来说,光的唯一性质就是速度 c,而物体的引力强度由 Gm 来表征,其中 G 是万有引力常数,m 是质量。此外,决定弯折多少的另一个量是光线靠物体有多近,即还要考虑一个特征距离 R。这个特征距离就是散射问题中的瞄准距,当光线从星体表面掠过时,瞄准距近似就是星体的半径。Gm,c …
是个无量纲量。就引力偏折光路这个问题来说,光的唯一性质就是速度 c,而物体的引力强度由 Gm 来表征,其中 G 是万有引力常数,m 是质量。此外,决定弯折多少的另一个量是光线靠物体有多近,即还要考虑一个特征距离 R。这个特征距离就是散射问题中的瞄准距,当光线从星体表面掠过时,瞄准距近似就是星体的半径。Gm,c …







